Schnell

	Einleitung
	Licht
	Schichten
	Zykloide
	Rechnung
	Ergebnis
	Modifikation
	Bau
	Versuch
	Ausstellung
	Mehr

Zykloide

An dieser Stelle soll zunächst das Ergebnis veranschaulicht werden. Die schnellste Bahn hat die Form einer Zykloide. Abhängig vom Zielpunkt wird die entsprechende Kurve nur bis dorthin durchlaufen. Im Bild ist eine ganze Schar von Zykloiden dargestellt. Im Startpunkt A verlaufen alle Kurven senkrecht nach unten. Durch jeden Punkt, der rechts von und tiefer als A liegt, gibt es genau eine Zykloide. Für Punkte links von A sähe es symmetrisch aus.

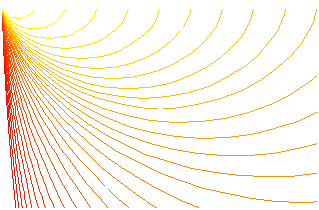
Der waagrechte Abstand zwischen Start- und Zielpunkt sei Δx, der senkrechte Abstand Δy. Es lassen sich folgende drei Fälle unterscheiden:

1. Zielpunkt B, Δx/Δy < π/2.
   Die Verbindung von A nach B ist ein wenig gebogen. Dieser Fall ist nicht besonders aufregend.
2. Zielpunkt C, Δx/Δy = π/2.
   Das ist der Sonderfall, bei dem C der tiefste Punkt der Zykloide ist, in dem sie waagrecht verläuft.
3. Zielpunkt D, Δx/Δy > π/2.
   In diesem verblüffenden Fall geht die Bahn tiefer runter als der Zielpunkt D liegt. Trotzdem ist diese Verbindung schneller als die Gerade von A nach D, ja sogar schneller als jede andere Kurve!

Wenn es also mal schnell gehen muss – ich meine natürlich, wenn eine Kugel so schnell wie möglich runter rollen soll – erinnerst du dich hoffentlich an die Brachistochrone.

Schichten

Rechnung