Schnell

	Einleitung
	Licht
	Schichten
	Zykloide
	Rechnung
	Ergebnis
	Modifikation
	Bau
	Versuch
	Ausstellung
	Mehr

Ergebnis

Mit der Gleichung

(13) t_AB = √(r / g) (p_B − p_A) .

kann man für beliebige Streckenabschnitte AB aus den zugehörigen Parameterwerten p_A und p_B die Laufzeit t_AB bestimmen. Weil diese Zeit proportional zur Parameteränderung ist, gleitet die Masse entlang der Zykloide genau so wie sich der Punkt auf dem erzeugenden Kreis bewegt, wenn dieser mit konstanter Geschwindigkeit abrollt. Alles klar? Das folgende Bild zeigt, was dieser Satz aussagen soll.

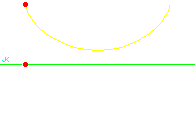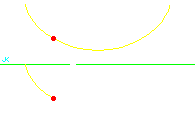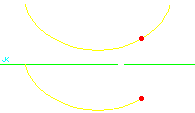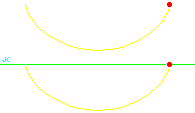
In der Animation ist die Gesamtzeit T = 2,4 s. Aus Gl. (13) folgt

(14) T = √(r / g) 2π

und aufgelöst nach r

(15) r = g (T / 2π)² .

Mit der Fallbeschleunigung von 9,81 m/s² auf der Erde entspricht die Zeit von 2,4 s einem Kreisradius von r = 1,43 m. Das gibt 'ne ziemlich große Zykloide, die horizontal 9 m breit wäre. Ob ich mich da irgendwo verrechnet habe?

Noch ein wichtiger Hinweis: Die obige Rechnung stimmt nur, wenn die Masse an der „Spitze“ der Zykloide losgelassen wird. Denn nur dann gilt der hergeleitete Zusammenhang zwischen der Geschwindigkeit v und der Höhe y Gl. (10) bzw. dem Parameter p Gl. (11).
Wie lange die Masse braucht, bis sie am tiefsten Punkt der Zykloide ankommt, wenn sie irgendwo anders auf der Kurve startet (nämlich immer gleich lang!) ist eine andere Frage. Zu diesem Problem gibt es etwas bei der Schaukel.

Rechnung

Modifikation