Schnell

	Einleitung
	Licht
	Schichten
	Zykloide
	Rechnung
	Ergebnis
	Modifikation
	Bau
	Versuch
	Ausstellung
	Mehr

Licht

Auch wenn man sich dessen meistens garnicht bewusst ist: Ein Lichtstrahl macht vor wie es geht. Er wählt ganz von selbst den schnellsten Weg, obwohl er gar nicht rechnen kann ;-)

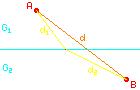
Der Einfachheit halber werden zunächst nur zwei Gebiete G₁ und G₂ betrachtet, in denen sich das Licht mit den Geschwindigkeiten v₁ bzw. v₂ ausbreitet. Der Lichtstrahl, der vom Punkt A startend durch den Punkt B geht, verläuft genau entlang der schnellsten Verbindung.
Das Problem etwas anschaulicher formuliert: Ein Auto fährt im Gebiet G₁ mit konstanter Geschwindigkeit v₁, im Gebiet G₂ mit konstanter Geschwindigkeit v₂. Wie muss eine Straße verlaufen, damit das Auto am schnellsten von A nach B kommt?

Innerhalb eines Gebietes mit konstanter Geschwindigkeit ist natürlich die gerade Verbindung auch die schnellste. Aber im Gebiet mit der höheren Geschwindigkeit darf der Weg etwas länger sein, wenn dadurch im Gebiet mit der niedrigen Geschwindigkeit der Weg verkürzt wird. Im Bild oben erkennt man, dass in diesem Fall die Gesamtstrecke d₁ + d₂ größer ist als die Entfernung d (Dreiecksungleichung). Es könnte also sein, dass der schnellste Weg an der Grenzlinie zwischen den beiden Gebieten abknickt. Und so ist es auch. Die Frage ist nur: An welcher Stelle genau muss der Knick sein?

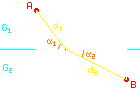
Weil ich gerade keine plausible Erklärung parat habe, folgt jetzt etwas Rechnerei. Falls dir mathematische Herleitungen nicht so viel Spaß machen, kannst du gleich direkt einen Blick auf das einfache Ergebnis Gl. (10) werfen.

Zunächst werden die vorkommenden Größen definiert. y₁ ist der Abstand des Punktes A von der Grenzlinie zwischen den Gebieten, entsprechend y₂ der Abstand des Punktes B. Die Entfernung der beiden Lotfußpunkte x_g wird in die beiden Teilstrecken x₁ und x₂ zerlegt.

(1) x_g = x₁ + x₂

Nach dem Satz von Pythagoras gilt

(2a) d₁ = √[x₁² + y₁²]
(2b) d₂ = √[x₂² + y₂²]

Mit Gl. (1) ergibt sich aus Gl. (2b)

(3) d₂ = √[(x_g − x₁)² + y₂²]

Aus den Weglängen d₁, d₂ und den zugehörigen Geschwindigkeiten v₁, v₂ ergeben sich die benötigten Zeiten t₁, t₂ zu

(4a) t₁ = d₁ / v₁ ,
(4b) t₂ = d₂ / v₂ .

Für die Gesamtzeit t_g gilt

(5) t_g = t₁ + t₂ .

Einsetzen der Gln. (2a, 3) in die Gln. (4a, 4b) und dieser in die Gl. (5) liefert

(6) t_g(x₁) = (1/v₁) √[x₁² + y₁²] + (1/v₂) √[(x_g − x₁)² + y₂²]

In dieser Gleichung sind alle Größen außer x₁ bekannt. Es ist derjenige Wert von x₁ gesucht, für den die Gesamtzeit t_g minimal wird. Eine notwendige Bedingung für ein lokales Extremum ist, dass die erste Ableitung von t_g nach x₁ verschwindet.

(7) dt_g/dx₁ = (1/v₁) (1/2) 1/√[x₁² + y₁²] 2x₁ +
(1/v₂) (1/2) 1/√[(x_g − x₁)² + y₂²] 2(x_g − x₁) (-1) = 0 .

Diese Gleichung nach x₁ aufzulösen, ist ziemlich aufwendig. Aber zum Glück ist das für das entscheidende Ergebnis gar nicht nötig. Nach Einsetzen der Gln. (2a, 3) und unter Berücksichtigung der Gl. (1) folgt

(8) (1/v₁) x₁ / d₁ = (1/v₂) x₂ / d₂ .

Aus dem Bild oben sieht man direkt

(9a) cos α₁ = x₁ / d₁ ,
(9b) cos α₂ = x₂ / d₂ .

Damit ergibt sich das schöne, einfache Ergebnis

(10) (cos α₁) / v₁ = (cos α₂) / v₂ .

Der Knick der Verbindungslinie erfolgt also derart, dass der Quotient aus dem Cosinus des Steigungswinkels und der Ausbreitungsgeschwindigkeit konstant bleibt.

Eine schöne Rechenübung für die Oberstufe des Gymnasiums ist die Bildung der zweiten Ableitung d²t_g/dx₁² ausgehend von Gl. (7). Die einzelnen Rechenschritte will ich hier nicht vorführen. Am Schluss kommt raus:

(11) d²t_g/dx₁² = (1/v₁) (d₁² - x₁²) / d₁³ + (1/v₂) (d₂² - x₂²) / d₂³ .

Alle auf der rechten Seite der Gleichung vorkommenden Größen sind positiv. Weiterhin ist

(12a) d₁ > x₁ ,
(12b) d₂ > x₂ .

Daher ist die zweite Ableitung immer positiv:

(13) d²t_g/dx₁² > 0 .

Die Extremstelle von t_g ist folglich ein Minimum, wie gewünscht.

Noch ein kleiner Einschub, um die Verwirrung komplett zu machen.

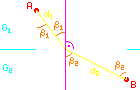
In der Optik werden normalerweise nicht die Steigungswinkel verwendet, sondern der Einfallswinkel β₁ und der Ausfallswinkel β₂, gemessen zum Lot im Knickpunkt. Dem obigen Bild ist direkt zu entnehmen, dass

(14a) sin β₁ = x₁ / d₁ ,
(14b) sin β₂ = x₂ / d₂ .

Mit Gl. (8) folgt daraus das Brechungsgesetz

(15) (sin β₁) / v₁ = (sin β₂) / v₂ .

Üblicherweise wird diese Gleichung noch nach sin β₁ / sin β₂ aufgelöst. Und statt den Geschwindigkeiten v₁ und v₂ werden die Brechzahlen n₁ und n₂ verwendet. Aber das ist jetzt wirklich eine Angelegenheit der Optik und führt zu weit weg von Kugelbahnen.

Einleitung

Schichten