Schnell

	Einleitung
	Licht
	Schichten
	Zykloide
	Rechnung
	Ergebnis
	Modifikation
	Bau
	Versuch
	Ausstellung
	Mehr

Rechnung

Vielen Dank Volker, dass du mir deine Facharbeit geschickt hast. Damit kein falscher Eindruck (insbesondere beim korrigierenden Lehrer) entsteht: Ich habe an dieser Stelle Informationen von ihm übernommen und nicht umgekehrt.

Zu beweisen, dass genau die Zykloide den schnellsten aller möglichen Wege liefert, ist ein Kapitel für sich. Das ist eher etwas für Kugelbahn-Fanatiker im fortgeschrittenen Stadium. Eine historische und eine moderne Herleitung beschreibt Ulrich Langenfeld.

Zum Einstieg geben wir einfach eine Zykloide vor und analysieren sie. Die Rechnung ist gar nicht so kompliziert, wenn man es richtig anstellt. Falls du die Einzelheiten der Herleitung überspringen willst, kannst du direkt zum interessanten Ergebnis mit Bild umblättern.

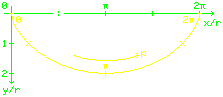
Um dieses Problem zu beschreiben, wählt man besser ein Koordinatensystem, in dem die y-Achse nach unten gerichtet ist. Die Zykloide wird durch folgende Gleichungen beschrieben:

(1) x = r (p − sin p) ,

(2) y = r (1 − cos p) .

Aufgepasst, es gibt verschiedene Möglichkeiten, Zykloiden-Gleichungen hinzuschreiben. Sie unterscheiden sich geringfügig, je nachdem wie das Koordinatensystem liegt und ob die „Spitzen“ der Zykloide oben oder unten sind. Die angegebenen Formeln passen zum gezeigten Bild. Der Kreisradius ist r, der Parameter p beschreibt den Drehwinkel, um den der Kreis abgerollt wurde.

Die Geschwindigkeit ist ja bekanntlich Strecke durch Zeit

(3) v = ds / dt .

Man muss das nur richtig interpretieren. Hier ist v die Geschwindigkeit in Bahnrichtung (tangential), ds ein (infinitesimal) kleines Stück der Kurve und dt der zugehörige Zeitabschnitt.

Berechnen wir zuerst die Länge ds. Für ein klitzekleines Kurvenstück gilt der Satz des Pythagoras:

(4) ds² = dx² + dy² .

Wenn man die Gln. (1) und (2) nach p differenziert, erhält man

(5) dx = r (1 − cos p) dp ,

(6) dy = r sin p dp .

Nach Einsetzen in Gl. (4) und Vereinfachen mit sin²p + cos²p = 1 ergibt sich

(7) ds = r √(2 − 2 cos p) dp .

Und jetzt kommt die Geschwindigkeit v dran. Wenn sich die Masse m um die Höhe y nach unten bewegt, wird gerade die potentielle Energie

(8) E_pot = m g y

in die kinetische Energie

(9) E_kin = 1/2 m v²

umgewandelt. Wenn keine Reibungsverluste auftreten, sind diese beiden Energien gleich und es folgt

(10) v = √(2 g y)

unabhängig von der Masse m. Und weiter mit Gl. (2)

(11) v = √(2 g r (1 − cos p) ) .

Jetzt ist ds und v bekannt und man kann Gl. (3) nach dt auflösen, die Gln. (7) und (11) einsetzen und vereinfachen.

(12) dt = ds / v = √(r / g) dp .

Was für ein glücklicher Zufall (oder war es Absicht?), dass in dieser Gleichung die Abhängigkeit von p herausgefallen ist. Die Zeit t_AB zwischen Punkt A und Punkt B ergibt sich durch Aufsummieren aller kleinen Zeitabschnitte dt. Dazu wird Gl. (12) von A bis B integriert. Weil √(r / g) unabhängig von p ist, kommt heraus

(13) t_AB = √(r / g) (p_B − p_A) .

Zykloide

Ergebnis