Welle

Steckbrief
Prinzip
> Steigung
Anschwingen
Exzenter

Steigung

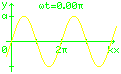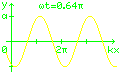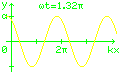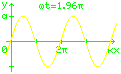
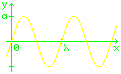
	Für die Kugelbahn ist der Sonderfall einer eindimensionalen harmonischen Welle interessant. y(x,t) = a sin (kx − ωt)
	Diese Gleichung beschreibt die Auslenkung y am Ort mit der Koordinate x zum Zeitpunkt t. Die Welle hat einen sinusförmigen Verlauf mit der Amplitude a, sowohl an einem festen Ort x in Abhängigkeit von der Zeit t, als auch zu einer festen Zeit t in Abhängigkeit vom Ort x. Das Minuszeichen in der Formel bewirkt, dass die Welle nach rechts läuft. Die Schwingungsdauer ist T = 2π/ω, die Wellenlänge λ = 2π/k. Für die Ausbreitungsgeschwindigkeit gilt v = λ/T = ω/k.
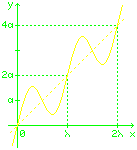
	Damit sich die Welle als Aufzug eignet, muss es noch irgendwie bergauf gehen. Das könnte man durch schräg stellen erreichen. In diesem Fall bewegen sich die einzelnen Stäbe (siehe Prinzip) jedoch nicht mehr senkrecht auf und ab und können leicht klemmen. Besser ist es, einen linearen Anstieg mx zu überlagern. y(x,t) = a sin (kx − ωt) + mx Die Steigung m > 0 darf nicht zu groß gewählt werden, damit Wellenberge und -täler erhalten bleiben. Das kann durch differenzieren obiger Gleichung nach x untersucht werden. dy/dx = ak cos (kx − ωt) + m
	Die Welle hat lokale Extrema (Minima oder Maxima) an den Stellen, an denen dy/dx null wird. Für jeden beliebigen Zeitpunkt t lässt sich ein x angeben, für das die cos-Funktion −1 wird. Daraus folgt, dass für m < ak die linear ansteigende Welle Berge und Täler besitzt. Für den Abstand Δx = λ ergibt sich damit ein möglicher Höhenanstieg von bis zu Δy = akλ = 2πa. Das heißt, pro Wellenlänge λ darf die Höhe bis zum 2π-fachen der Amplitude a zunehmen. Wenn man geringe Höhenverluste beim Übergang zwischen zwei Stäben einplant, erscheint ein Wert von fünf realistisch. Das führt zu erstaunlich steilen Anstiegen bis zur fünffachen Amplitude pro Wellenlänge. 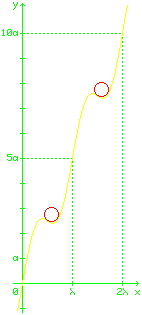Die nebenstehende Zeichnung zeigt den Verlauf für die typischen Werte Kugeldurchmesser 15, Wellenlänge λ = 50, Amplitude a = 25, Steigung m = 2.5. Als Einheit kannst du Pixel oder Millimeter oder was auch immer du willst nehmen, das spielt keine Rolle.

Prinzip

Anschwingen